Davide Bombacigno

Interested in solutions, and people

Analysis of videogames market, biggest market and best selling genres

We will analyze the sales data of the videogames market using the data about games with more than 100000 copies sold

source: https://www.kaggle.com/gregorut/videogamesales Code and data used: https://github.com/davbom97/source

I assume this data to be somewhat representative sample of the videogames market and I will use it to extract some insights

  • Import Data
  • Data Cleaning
  • Data Analysis
    • Composition of Total Sales by Market
    • Time series of Sales by Market
    • Markets composition by Genre
    • Analysis of Genre Sales
      • Genre sales boxplot
      • Which Genre sells the most per game?
import pandas as pd
import numpy as np
from IPython.display import display,Image
import plotly.graph_objs as go
from plotly.subplots import make_subplots
import plotly.figure_factory as ff
import plotly.express as px

Import Data

data = pd.read_csv("vgsales.csv").sort_values("Global_Sales",ascending= False)
data = data.drop("Rank",axis = 1)

display(data.head(5))
Name Platform Year Genre Publisher NA_Sales EU_Sales JP_Sales Other_Sales Global_Sales
0 Wii Sports Wii 2006.0 Sports Nintendo 41.49 29.02 3.77 8.46 82.74
1 Super Mario Bros. NES 1985.0 Platform Nintendo 29.08 3.58 6.81 0.77 40.24
2 Mario Kart Wii Wii 2008.0 Racing Nintendo 15.85 12.88 3.79 3.31 35.82
3 Wii Sports Resort Wii 2009.0 Sports Nintendo 15.75 11.01 3.28 2.96 33.00
4 Pokemon Red/Pokemon Blue GB 1996.0 Role-Playing Nintendo 11.27 8.89 10.22 1.00 31.37

The data reports for each game:

  • The game name (Unique for every game)
  • The main platform it was published (Categorical value)
  • Year it was bublished (Numeric discrete value)
  • Its genre (Categorical value)
  • Its publisher (Categorical value)
  • Sales by market (Numeric continuous value)

Entries are ranked by descending order of global sales

Data Cleaning

Because the data is incomplete from 2016 on, we drop all the entries beyond 2015

data = data[data["Year"] <= 2015]

Then we check if there are any NaN values in the data

data_na = data.isna().sum()
display(data_na)

Name             0
Platform         0
Year             0
Genre            0
Publisher       34
NA_Sales         0
EU_Sales         0
JP_Sales         0
Other_Sales      0
Global_Sales     0
dtype: int64

There seems to be some missing values in the “Publisher” category, may be due some minor publishers

Becouse there are only 34 missing values, I decided to delete those entries

data = data.dropna()

Data Analysis

Composition of Total Sales by Market

We group the sales by year and market to find which one contributes the most to the total sales

market_data = data[["Year","NA_Sales","EU_Sales","JP_Sales","Other_Sales"]].groupby("Year").sum()
display(market_data.head(5))
NA_Sales EU_Sales JP_Sales Other_Sales
Year
1980.0 10.59 0.67 0.00 0.12
1981.0 33.40 1.96 0.00 0.32
1982.0 26.92 1.65 0.00 0.31
1983.0 7.76 0.80 8.10 0.14
1984.0 33.28 2.10 14.27 0.70

There seems to be missing data of JP_Sales from 1980 to 1982, so we drop these years for the analysis

market_data = market_data[market_data.index >1982]

display(market_data.sum().reset_index())
fig = px.pie(market_data.sum().reset_index(),values = 0,names = "index")
fig.update_layout(title="Global Sales composition by Market")
img_bytes = fig.to_image(format="png")
Image(img_bytes)
index 0
0 NA_Sales 4233.81
1 EU_Sales 2375.65
2 JP_Sales 1270.55
3 Other_Sales 780.39

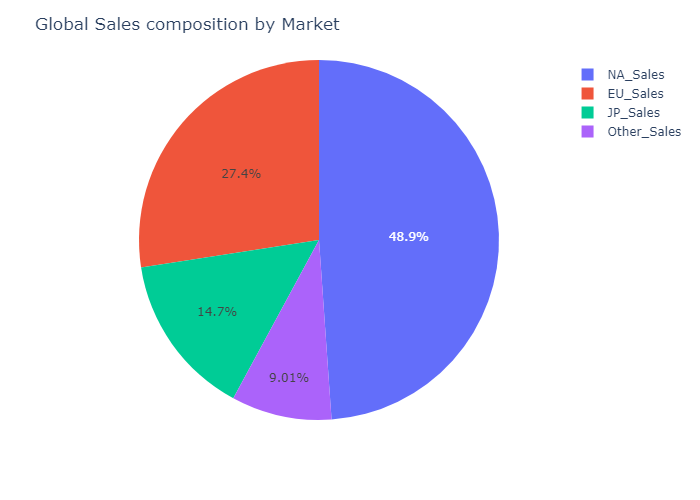
output_22_1.png

From the data emerges that the biggest market is the North American one, making up to almost the 50% of the total sales, followed by the European and the Japanese ones.

Time series of Sales per Market

Now we want to see the time series of the total sales and the sales per market

fig = go.Figure()

fig.add_trace(go.Scatter(x = market_data.index, y= market_data.sum(axis = 1), mode = "lines+markers"))

fig.update_layout(title="Time Series of Total Sales",
                   xaxis_title="Total Sales (Mln)",
                   yaxis_title="Year")
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

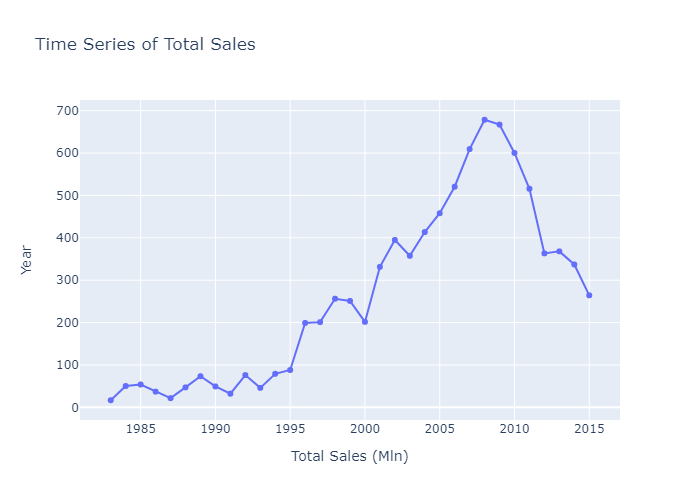
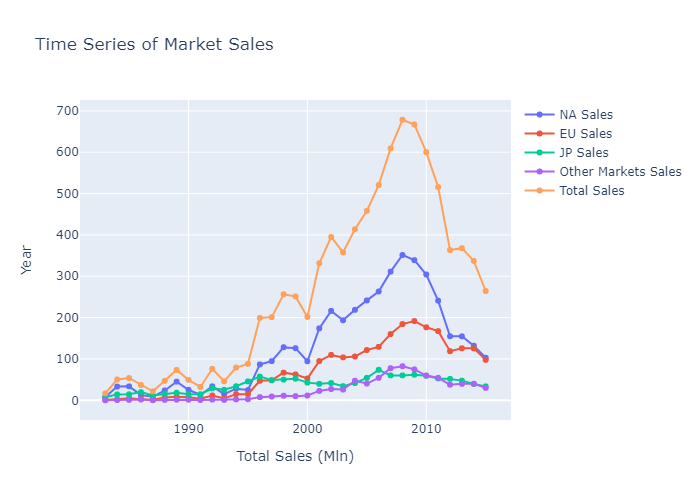
fig = go.Figure()
fig.add_trace(go.Scatter(x = market_data.index, y= market_data["NA_Sales"], name = "NA Sales", mode = "lines+markers"))
fig.add_trace(go.Scatter(x = market_data.index, y= market_data["EU_Sales"], name = "EU Sales", mode = "lines+markers"))
fig.add_trace(go.Scatter(x = market_data.index, y= market_data["JP_Sales"], name = "JP Sales", mode = "lines+markers"))
fig.add_trace(go.Scatter(x = market_data.index, y= market_data["Other_Sales"], name = "Other Markets Sales", mode = "lines+markers"))
fig.add_trace(go.Scatter(x = market_data.index, y= market_data.sum(axis = 1), name = "Total Sales" ,mode = "lines+markers"))
fig.update_layout(title="Time Series of Market Sales",
                   xaxis_title="Total Sales (Mln)",
                   yaxis_title="Year")
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

market_sales_change = (market_data.pct_change()*100).round(2)
total_sales_change = (market_data.sum(axis = 1).pct_change()*100).round(2)

fig = make_subplots(rows=5, cols=1, shared_yaxes = True)
fig.add_trace(go.Scatter(x = market_sales_change.index, y= market_sales_change["NA_Sales"], name = "NA Sales", mode = "lines+markers"),row =1,col = 1)
fig.add_trace(go.Scatter(x = market_sales_change.index, y= market_sales_change["EU_Sales"], name = "EU Sales", mode = "lines+markers"),row =2,col = 1)
fig.add_trace(go.Scatter(x = market_sales_change.index, y= market_sales_change["JP_Sales"], name = "JP Sales", mode = "lines+markers"),row =3,col = 1)
fig.add_trace(go.Scatter(x = market_sales_change.index, y= market_sales_change["Other_Sales"], name = "Other Markets Sales", mode = "lines+markers"),row =4,col = 1)
fig.add_trace(go.Scatter(x = total_sales_change.index, y= total_sales_change, name = "Total Sales" ,mode = "lines+markers"),row =5,col = 1)
fig.update_layout(title="Rate of change of Market Sales",
                   xaxis_title="Year",
                   yaxis_title="Rate of change (%)",
                   height=800)
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

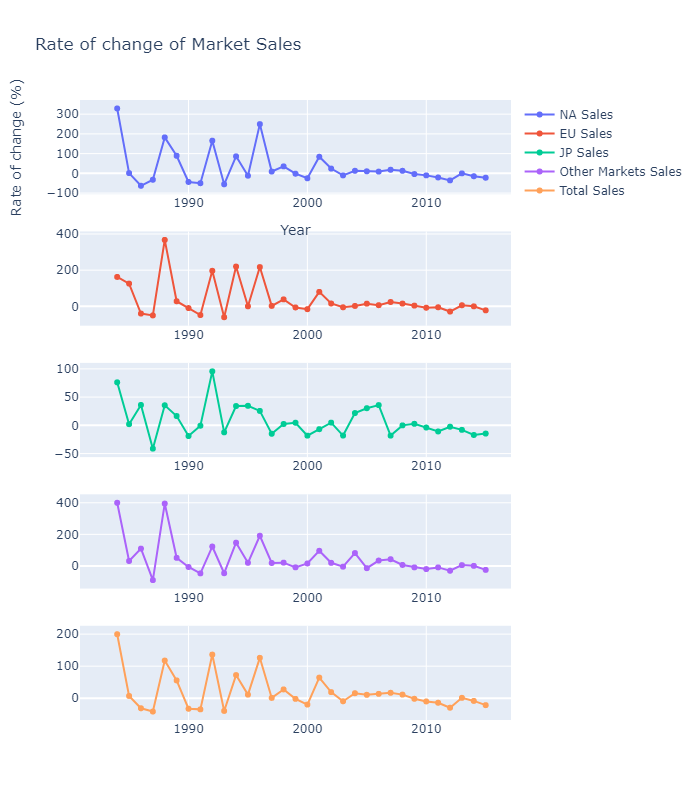
The data shows the growth of the videogames markets and the effects of the economic cycles and bubbles (the dot-com bubble in 2000, the crisis of 2008 on the NA sales and the European debt crisis of 2010-2011 on the EU markets).

In general, the market peaked in 2008, right before the economi crisis of those years, while showing a down trend in 2015.

While it is obvious the impact of the economic cycle on the sales, it must be noted that some changes in the industry might have shifted the focus of the companies and the customers(Microtransactions, DLCs, Free to Play business models, etc), indicating that the reduction of sales does not mean that the industry is in a bad shape, but just that now there are more revenue sources for the companies besides game sales than in the past.

Looking at the average growth rates of each market:

display(market_sales_change.mean().round(2))

NA_Sales       28.72
EU_Sales       38.28
JP_Sales        7.88
Other_Sales    46.86
dtype: float64

And the total sales growth rate:

display("The total sales average growth rate is : %.2f" % total_sales_change.mean())

'The total sales average growth rate is : 19.10'

Markets composition by Genre

Now we can see which are the best selling genres and platforms for each market using a heatmap:

market_sales_genre = data.drop(["Global_Sales","Year"], axis = 1).groupby("Genre").sum()
market_sales_genre = (market_sales_genre.div(market_sales_genre.sum(axis = 0),axis = 1)*100).round(2)
fig = ff.create_annotated_heatmap(z = market_sales_genre.values,
                                  y = market_sales_genre.index.values.tolist(),
                                  x = market_sales_genre.columns.values.tolist())
fig.update_layout(title="Composition of each market by genre (%)")
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

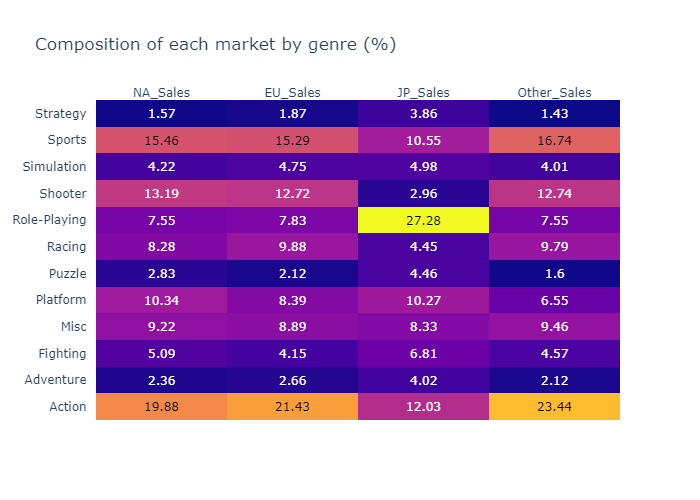
print("The top 3 selling genres in the NA market are:")
print(market_sales_genre["NA_Sales"].sort_values(ascending = False)[:3])

print("\nThe top 3 selling genres in the EU market are:")
print(market_sales_genre["EU_Sales"].sort_values(ascending = False)[:3])

print("\nThe top 3 selling genres in the JP market are:")
print(market_sales_genre["JP_Sales"].sort_values(ascending = False)[:3])

print("\nThe top 3 selling genres in other markets are:")
print(market_sales_genre["Other_Sales"].sort_values(ascending = False)[:3])

The top 3 selling genres in the NA market are:
Genre
Action     19.88
Sports     15.46
Shooter    13.19
Name: NA_Sales, dtype: float64

The top 3 selling genres in the EU market are:
Genre
Action     21.43
Sports     15.29
Shooter    12.72
Name: EU_Sales, dtype: float64

The top 3 selling genres in the JP market are:
Genre
Role-Playing    27.28
Action          12.03
Sports          10.55
Name: JP_Sales, dtype: float64

The top 3 selling genres in other markets are:
Genre
Action     23.44
Sports     16.74
Shooter    12.74
Name: Other_Sales, dtype: float64

Composition of Total Sales by Genre

Like we did for the markets, we group the sales by Genre and Year:

genre_sales = data[["Year","Genre","Global_Sales"]].groupby(["Year","Genre"]).sum().unstack(level=-1).droplevel(0,axis = 1)
display(genre_sales.head(12))
Genre Action Adventure Fighting Misc Platform Puzzle Racing Role-Playing Shooter Simulation Sports Strategy
Year
1980.0 0.34 NaN 0.77 2.71 NaN NaN NaN NaN 7.07 NaN 0.49 NaN
1981.0 14.84 NaN NaN NaN 6.93 2.24 0.48 NaN 10.04 0.45 0.79 NaN
1982.0 6.52 NaN NaN 0.87 5.03 10.03 1.57 NaN 3.79 NaN 1.05 NaN
1983.0 2.86 0.40 NaN 2.14 6.93 0.78 NaN NaN 0.48 NaN 3.20 NaN
1984.0 1.85 NaN NaN 1.45 0.69 3.14 5.95 NaN 31.10 NaN 6.18 NaN
1985.0 3.52 NaN 1.05 NaN 43.17 3.21 NaN NaN 1.00 0.03 1.96 NaN
1986.0 13.74 NaN NaN NaN 9.39 NaN 1.96 2.52 3.89 NaN 5.57 NaN
1987.0 1.12 4.38 5.42 NaN 1.74 NaN NaN 4.65 0.71 NaN 3.72 NaN
1988.0 1.75 NaN NaN NaN 27.73 5.58 2.14 5.88 0.51 0.03 3.60 NaN
1989.0 4.64 NaN NaN 1.28 20.66 37.75 NaN 2.20 1.20 NaN 5.72 NaN
1990.0 6.39 NaN NaN NaN 22.97 6.00 6.26 4.52 NaN 1.14 2.11 NaN
1991.0 6.76 2.24 0.39 0.08 7.64 3.24 1.14 3.25 2.00 2.14 2.41 0.94

There are missing values (probably due to the genre not being defined at the time, or not existing), so we delete all the entries before 1991.

genre_sales = genre_sales[genre_sales.index >= 1991]

fig = px.pie(genre_sales.sum(),values = 0,names = genre_sales.columns)
fig.update_layout(title="Global Sales composition by Genre")
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

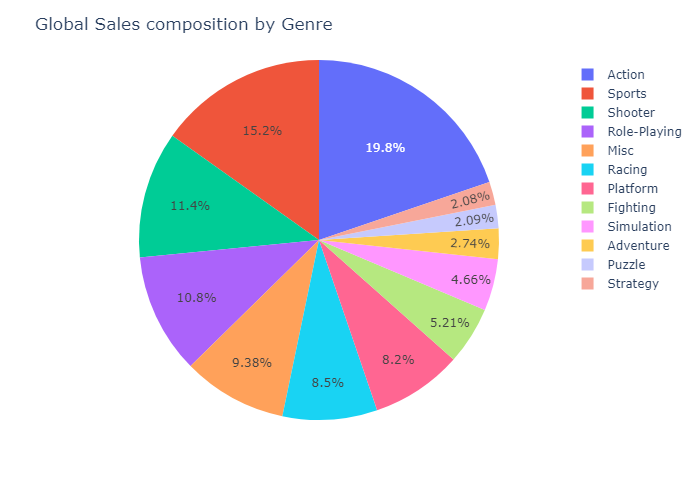
Here we can see that the best selling Genres are:

  • Action
  • Sports
  • Shooter and Role-Playing

Analysis of Genre Sales

We want to ask ourselves “Which Genres are, on average, the best selling?”

Looking at the total sales does not tell us the full story, because the most of sales are done only by few very big hits and are dependent on the count of games relased:

data_1991_on = data[data["Year"]>=1991]
genre_sales_desc = data_1991_on[["Genre","Global_Sales"]].groupby("Genre").describe().droplevel(0,axis = 1)
genre_sales_desc = genre_sales_desc.sort_values(by =["50%"],axis = 0,ascending = False)
display(genre_sales_desc)
count mean std min 25% 50% 75% max
Genre
Platform 829.0 0.822461 2.005954 0.01 0.090 0.250 0.6900 30.01
Shooter 1220.0 0.777205 1.692879 0.01 0.080 0.220 0.7100 14.76
Sports 2240.0 0.562612 2.127120 0.01 0.090 0.220 0.5525 82.74
Fighting 818.0 0.529279 0.960339 0.01 0.080 0.210 0.5500 13.04
Action 3063.0 0.537173 1.185337 0.01 0.070 0.190 0.5000 21.40
Racing 1195.0 0.591431 1.689209 0.01 0.075 0.190 0.5300 35.82
Role-Playing 1417.0 0.633211 1.741657 0.01 0.070 0.190 0.5300 31.37
Misc 1660.0 0.470030 1.340625 0.01 0.060 0.160 0.4100 29.02
Simulation 834.0 0.464808 1.216313 0.01 0.060 0.160 0.4300 24.76
Puzzle 549.0 0.315993 0.839252 0.01 0.040 0.100 0.2700 15.30
Strategy 660.0 0.261773 0.527860 0.01 0.040 0.095 0.2800 5.45
Adventure 1239.0 0.184036 0.503521 0.01 0.020 0.060 0.1600 11.18

Looking at the histogram of the distribution of global sales for all games:

fig = px.histogram(data_1991_on["Global_Sales"], x="Global_Sales", nbins=50)
fig.update_layout(title="Histogram of the distribution of Global Sales",
                   xaxis_title="Global Sales")
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

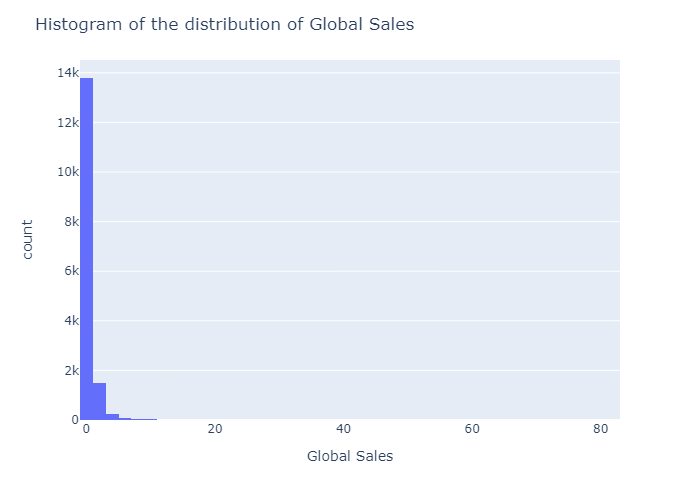
Calculating the 95th percentile:

print("The 95th percentile is equal to : %f" % (data_1991_on["Global_Sales"].quantile(0.95)))

The 95th percentile is equal to : 2.008500

Meaning that the 95% of games in this sample made less than 2 milion copies sold

relative_total = 0
i = 0
total = data_1991_on["Global_Sales"].sum()
sales = data_1991_on[["Global_Sales"]]
pareto = []
while relative_total <= 0.8:
    game_sales_perc = data_1991_on["Global_Sales"].iloc[i]/total
    relative_total += game_sales_perc
    i+=1
print("The %f%% of games makes up for the %f%% of sales" % (i/len(sales)*100, relative_total*100))


The 25.572373% of games makes up for the 80.003392% of sales

Another evidence of the skewness is that just around 25% percent of games make the 80% total sales

Genre Sales boxplot

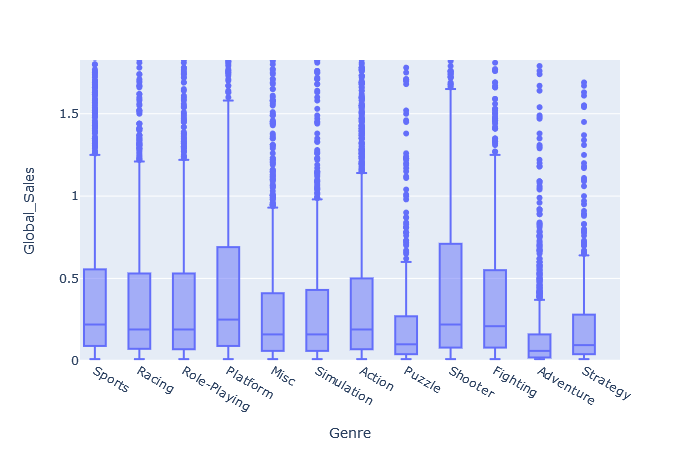
Within every Genre there is a huge variance, in support of our hypothesis we can see that the median sales are lower than the average sales, it is even more evident with a boxplot:

fig = px.box(data_1991_on, y="Global_Sales",x = "Genre")
img_bytes = fig.to_image(format="png")
Image(img_bytes)

png

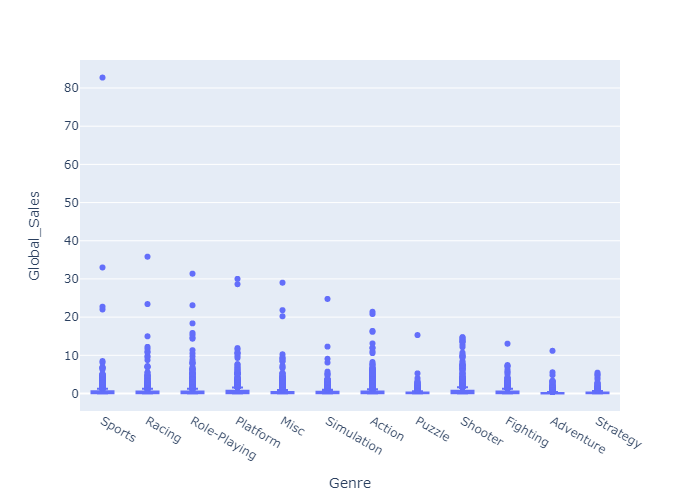
The outliers (best selling games) make the boxplot unreadable, zooming in the boxes:

Image(filename="boxplot_zoomed.png")

png

Which Genre sells the most per game?

To answer this question we have to take in account the variability within each genre, thus we will evaluate the best selling genre per game using the quartile coefficient of dispersion:

genre_sales_qcd = ((genre_sales_desc["75%"]-genre_sales_desc["25%"])/(genre_sales_desc["75%"]+genre_sales_desc["25%"])).sort_values(ascending = False)
print("The quartile coefficient of dispersion for each Genre is:")
display(genre_sales_qcd)

fig = go.Figure(go.Bar(x = genre_sales_qcd.index, y = genre_sales_qcd.values, text = genre_sales_qcd.round(2),textposition='outside'))
fig.update_layout(title="Quartile coefficient of dispersion",
                   yaxis_title="qcd",
                   height=500)
img_bytes = fig.to_image(format="png")
Image(img_bytes)

The quartile coefficient of dispersion for each Genre is:



Genre
Shooter         0.797468
Adventure       0.777778
Platform        0.769231
Role-Playing    0.766667
Simulation      0.755102
Action          0.754386
Racing          0.752066
Strategy        0.750000
Fighting        0.746032
Misc            0.744681
Puzzle          0.741935
Sports          0.719844
dtype: float64

png

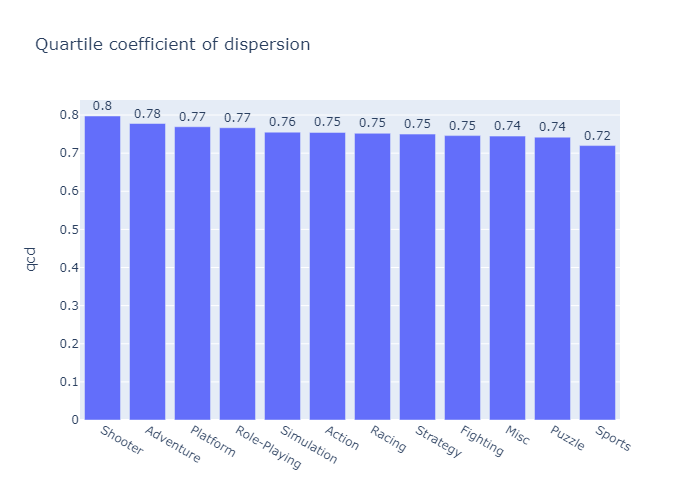
Note: When comparing two genres, the one with the less coefficient of variation has lower variability between each game

Now, as written above, on average the best selling genres are:

  • Platform
  • Shooter
  • Sports
for genre in genre_sales_desc.index[:3]:
    print("The Genre %s qcv: %f median : %f" %(genre, genre_sales_qcd.loc[genre],genre_sales_desc.loc[genre]["50%"]))

The Genre Platform qcv: 0.769231 median : 0.250000
The Genre Shooter qcv: 0.797468 median : 0.220000
The Genre Sports qcv: 0.719844 median : 0.220000

Conclusions

Among the videogames markets, the NA is the biggest one, followed by EU and JP

The most sold Genres are Action, Sports, Shooter, and make up a significant portion of videogames sales in each market, with the exeption of Role-Playing, which is sold a lot in the JP market, making up the 27.3% of sales alone in that market.

Looking at the median copies sold by each game within a genre, We have that the Platform, Shooter and Sports games are on average the best selling, the median of the Platform genre in bigger than the Shooter one, while having a smaller quartile coefficient of dispersion, meaning that it has a lower variability of copies sold from game to game, meaning that overall the Platform Genre is better selling than the Shooting Genre.

The Shooter Genre has a equal median and a bigger qcd than the Sports, meaning that they sell on average the same, but the Shooter has more variability in sales, thus concluding that the top three selling Genres, on average, are in order:

  • Platform
  • Sports
  • Shooter

2020

Back to top ↑

2019

Single facility location problem

6 minute read

In this post we will find out how to choose the best location for a single uncapacitated facility given a set of points of interest

Back to top ↑